Sin/cos generation using table lookup and interpolation.

Introduction

In the past, I’ve written several blog posts on calculating sin(x) and cos(x) using polynomials. These methods can be very accurate but require many multiplications and additions. For usage in hand-held calculators, where a few evaluations per second are enough, these algorithms are fine. However, in high-speed signal processing and generation applications, such as software-defined radio or test equipment, a less computationally intensive method is required.

A simple way to generate waveforms is to read the contents of a table, which resides in memory, at a constant speed. Usually, a single cycle of the desired waveform is stored in the table. When the table has number of entries and the table entries are read at a speed of entries per second, the frequency of the generated waveform will be Hz.

Algorithm #1: Table lookup

To generate a sine (or cosine) wave, we must simply fill the table with sin(x). The table entries are thus: .

/* Get integer types with well-defined number of bits */
#include <stdint.h>
#include <stdio.h>
#include <math.h>
 
/* Define a table of 256 entries containing a single cycle waveform.
   The table entries are not shown.
*/
float table[256];

/* Fill the table with a single sin(x) cycle */
void fillTable()
{
    for(uint32_t i=0; i<256; i++)
        table[i] = sin(2.0*3.1415927*(float)i/256.0);
}

int main(int, char**)
{
    uint32_t sampleRate=1000;    // sample rate of 1000 samples-per-second
    uint32_t desiredFreq=199;    // desired generated frequency
    uint32_t phaseAccumulator=0; // fixed-point (16.16) phase accumulator 

    fillTable();
     
    /* fixed-point (16.16) phase increment */
    uint32_t phaseIncrement=(256*65536*desiredFreq/sampleRate);
     
    while(true)        // loop forever
    {
      /* Increment the phase accumulator */
      phaseAccumulator += phaseIncrement;
     
      /* Limit the phase accumulator to 24 bits.
         The lower 16 bits are the fractional table
         index part, while the remaining 8 bits
         are the integer index into the waveform
         table.
      */
      phaseAccumulator &= (256*65536)-1;              
     
      /* Read the table by removing right shifting
         the lowest (fractional) bits into oblivion
         and we are left with the remaining 8 bits.
         This truncates the table index, without
         rounding. */
      uint32_t tableIndex = phaseAccumulator >> 16;
      printf("%f\n", table[tableIndex]);
    }
}

The code above will generate a sine wave and print the result to the console. The phase accumulator technique is basically an counter that periodically “overflows”, i.e. restarts, when the end of the table is reached. This is done by removing the highest bits from the 32-bit integer. For each new output sample, the phase accumulator is increased by the phase increment. The phase increment determines the frequency. This way, the frequency produced is independent from the number of table entries.

Which entry from the table is read is determined by bit-shifting the phase accumulator to the right by 16, which effectively removes the lower 16 bits from the 24-bit accumulator, leaving an 8-bit table index. The index will therefore always be within 0 .. 255!

The lower 16 bits of the phase accumulator represent the desired read position of the waveform “between” the table entries. In the example code above, this information is discarded. We will come back to this later.

Evaluation: Algorithm #1

To evaluate the spectral purity of the generated sine wave, the output of the example program was analyzed using the FFT. The following plot shows the results:

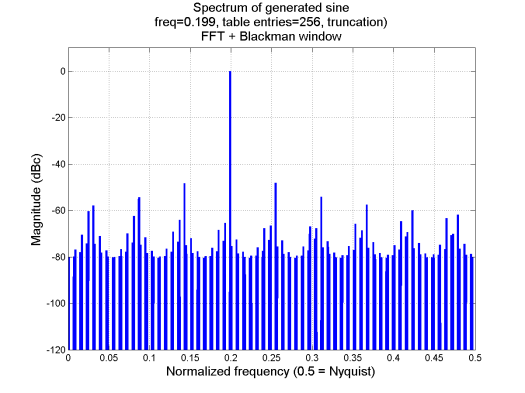The spectral purity of the signal is not spectacular, to say the least. There are strong spurious responses as high as -50 dBc. Relatively large errors are produced because of the finite length of the table.

Algorithm #2: Table lookup and interpolation

We can easily get better results without increasing the number of table entries significantly by interpolating between the table values; we have the fractional part! The following algorithm uses linear interpolation:

/* Get integer types with well-defined number of bits */
#include <stdint.h>
#include <stdio.h>
#include <math.h>
 
/* Define a table of 257! entries containing a single cycle waveform.
   The additional table entry makes sure that table[index+1] never
   causes an out-of-bound read.

   The table entries are not shown.
   Note: we now set table[256] = table[0]!
*/
float table[257];

/* Fill the table with a single sin(x) cycle */
void fillTable()
{
    for(uint32_t i=0; i<256; i++)
        table[i] = sin(2.0*3.1415927*(float)i/256.0);
    table[256] = table[0];
}

int main(int, char**)
{
    uint32_t sampleRate=1000;    // sample rate of 1000 samples-per-second
    uint32_t desiredFreq=199;    // desired generated frequency
    uint32_t phaseAccumulator=0; // fixed-point (16.16) phase accumulator 

    fillTable();
     
    /* fixed-point (16.16) phase increment */
    uint32_t phaseIncrement=(256*65536*desiredFreq/sampleRate);
     
    while(true)        // loop forever
    {
      /* Increment the phase accumulator */
      phaseAccumulator += phaseIncrement;
     
      /* Limit the phase accumulator to 24 bits.
         The lower 16 bits are the fractional table
         index part, while the remaining 8 bits
         are the integer index into the waveform
         table.
      */
      phaseAccumulator &= (256*65536)-1;              
     
      /* Calculate the table index. */
      uint32_t index = phaseAccumulator >> 16;

      /* Get the table entry and the one
         directly following it.
      */
      float v1 = table[index];
      float v2 = table[index+1];

      /* turn the fixed-point fractional part into
         a float-point representation so we can
         use it. */
      float fmul = static_cast<float>(phaseAccumulator & 65535)/65536.0f;

      /* perform the linear interpolation */
      float out = v1 + (v2-v1)*fmul;

      printf("%f\n", out);
    }
}

Evaluation: Algorithm #2

Using the same method as earlier, the performance of the algorithm is evaluated, resulting in the following figure:

Clearly, the linear interpolation increases the spectral purity significantly! There are fewer spurious responses and the highest one is better than -90 dBc. For software radio applications this good enough.

Algorithm #3: Table lookup and circular interpolation

There are certain applications where -90 dBc of spectral purity isn’t enough, for instance, in test equipment, very high purity digital down-converters are needed for precise measurements, e.g. to reduce noise folding. To increase the spectral purity, we could increase the table size, or we could choose a better interpolation method.

One way of getting a better interpolation method would be to use following identity:

If we choose A to be derived from the upper 8 bits (integer part) of the phase accumulator, we can lookup and using our table and these lookups will be exact. Note that , so is simply found 64 entries further in the table. Then, B is the fractional angle, which is represented by the lower 16 bits of the phase accumulator. As the fractional angle is always somewhere between the table entries, we cannot use our lookup table. We could use a second lookup table or we can use the well-known approximations of and for small angles:

and .

The following code example uses this principle:

/*Get integer types with well-defined number of bits */
#include <stdint.h>
#include <stdio.h>
#include <math.h>
/* Define a table of 256 entries containing a single cycle waveform.
   The table entries are not shown.
*/
float table[256];

/* Fill the table with a single sin(x) cycle */
void fillTable()
{
    for(uint32_t i=0; i<256; i++)
        table[i] = sin(2.0*3.1415927*(float)i/256.0);
}

int main(int, char**)
{
    uint32_t sampleRate=1000;    // sample rate of 1000 samples-per-second
    uint32_t desiredFreq=199;    // desired generated frequency
    uint32_t phaseAccumulator=0; // fixed-point (16.16) phase accumulator
    fillTable();
    /* fixed-point (16.16) phase increment */
    uint32_t phaseIncrement=(256*65536*desiredFreq/sampleRate);

    //while(true)        // loop forever
    for(uint32_t i=0; i<65536; i++)
    {
      /* Increment the phase accumulator */
      phaseAccumulator += phaseIncrement;
      /* Limit the phase accumulator to 24 bits.
         The lower 16 bits are the fractional table
         index part, while the remaining 8 bits
         are the integer index into the waveform
         table.
      */
      phaseAccumulator &= (256*65536)-1;

      /* Calculate the table index. */
      uint32_t index = phaseAccumulator >> 16;

      /* Get the table entry and the one
         directly following it.
      */
      float v_sin = table[index];
      float v_cos = table[(index+64) & 255];
      float frac  = 2.0f*3.1415927f*static_cast<float>(phaseAccumulator & 65535)/65536.0f/256.0f;

      // fractional sin/cos
      float f_sin = frac;
      float f_cos = 1.0f - 0.5f*frac*frac;

      float result = v_sin*f_cos + v_cos*f_sin;
      printf("%f\n", result);
    }
}

Evaluation: Algorithm #3

Again, the waveform was evaluated. The results are shown in the figure below:

The circular interpolation gives an improvement over linear interpolation at the cost of an additional table lookup and a few multiplications and additions. The spurious responses are now found at around -128 dBc, which is 38 dB better.

Further experiments show that increasing the table size to 512 entries produces spurious responses that are below -147 dBc. A table size of 128 entries gives responses below -110 dBc.

Conclusions

The table-lookup and interpolate method of signal generation is a powerful way to generate high-purity signals without resorting to complex approximations.With simple linear interpolation, a 256-entry table can produce sine and cosine waveforms with spurious responses that are around 90 dB below the carrier. At the expense of a few additional operations, spurious responses can be as low as -128 dBc by using circular interpolation.

The presented algorithms are also well suited to generate quadrature signals as both sine and cosine waveforms can be generated simultaneously.